Modalidade de funcionamento do seminário no semestre 2022.1
No semestre 2022.1, as palestras públicas do Seminário ICmat ocorrerão ainda online, usando o aplicativo Google Meet, preferencialmente nas segundas-feiras, das 17:00 às 18:00. Ocasionalmente, as palestras poderão ocorrer em outros dias e horários.
Para participar
Este seminário é destinado unicamente aos estudantes. Os estudantes interessados em participar do seminário deverão realizar um cadastro por meio do seguinte Formulário.
Para ministrar palestras
Os alunos interessados em apresentar uma palestra podem encaminhar uma proposta para seminarioICmat@gmail.com.
Próximas palestras
-
Segunda-feira 4 de julho - 17:00 horas (Sala virtual Google Meet)
(O link da palestra será enviado por email aos interessados)
Titulo: Método de Hamilton - Jacobi : desmistificando a arte de escolher boas coordenadas
Palestrante: Juliana Medeiros Barbosa (aluno do curso de graduação em matemática - UFBA)
Orientador: Diego Catalano Ferraioli (UFBA)
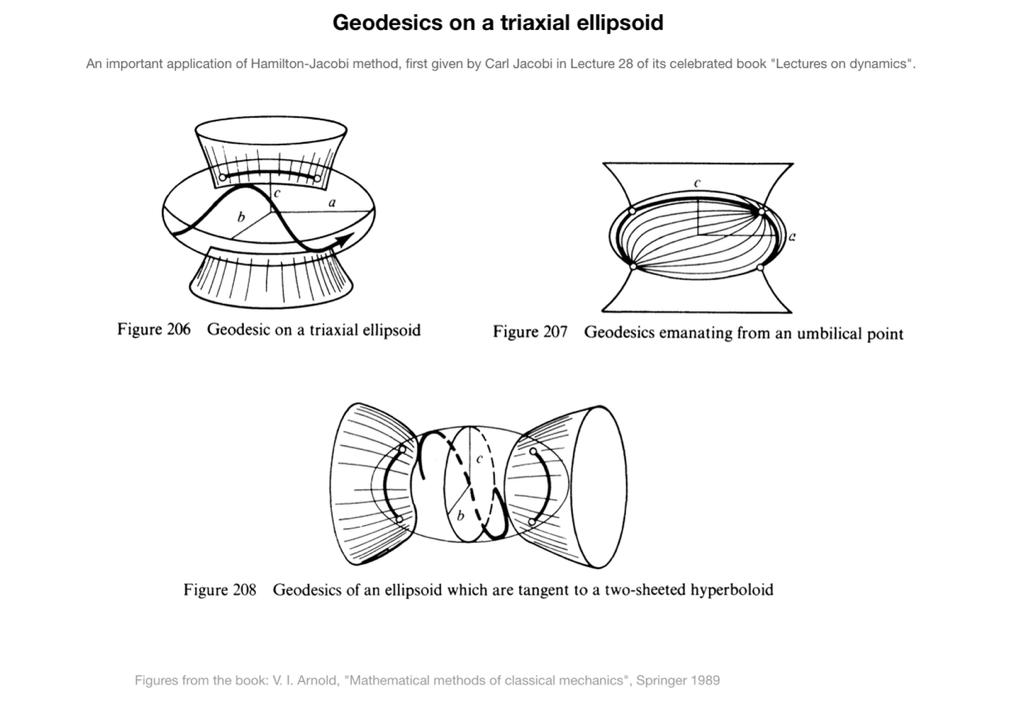
Resumo: Apesar de representar um marco fundamental na compreensão do universo, a formulação newtoniana tradicional nem sempre é suficiente para nossa compreensão de alguns sistemas mecânicos. Nos casos em que é possível uma descrição variacional, as formulações Lagrangeana e Hamiltoniana apresentam inúmeras vantagens, que essencialmente derivam da possibilidade de explorar melhor, de um lado, o papel de algumas estruturas geométricas características das equações diferenciais da mecânica e, do outro lado, o papel fundamental das simetrias (de vários tipos) apresentadas por estes sistemas. Esta teoria, inicialmente desenvolvida para problemas mecânicos, representa um capítulo particularmente importante da teoria mais geral das equações diferenciais ordinárias, que possui aplicações também em outros âmbitos como, por exemplo, o estudo das geodésicas em uma superfície. Nesta palestra, depois de uma introdução ao formalismo Hamiltoniano, discutiremos o papel desempenhado pela geometria na identificação de um método (Hamilton-Jacobi) que permite de determinar coordenadas particularmente boas, em termos das quais as equações diferenciais do sistema mecânico podem ser facilmente resolvidas.
Moderador da palestra: João Mark Souza Oliveira
Palestras já realizadas
-
Segunda-feira 27 de junho - 17:00 horas (Sala virtual Google Meet)
(O link da palestra será enviado por email aos interessados)
Titulo: Invariantes de Nós e Enlaçamentos
Palestrante: Gustavo Cardoso (aluno do curso de graduação em matemática - UFBA)
Orientador: Oscar Ocampo (UFBA)
Resumo: A teoria de nós e enlaçamentos é um dos tópicos clássicos da topologia de baixa dimensão. Nessa teoria, uma das questões mais naturais que surgem é: Como garantir que dois nós ou enlaçamentos são distintos? Uma das maneiras de responder a essa pergunta é através dos invariantes, que irão associar objetos geométricos (nós ou enlaçamentos) a objetos algébricos (como números ou polinômios). Nesta palestra, abordaremos dois desses invariantes: o Polinômio de Kauffman e o Polinômio de Jones.
Moderador da palestra: Juliana Medeiros Barbosa
-
Segunda-feira 20 de junho - 17:00 horas (Sala virtual Google Meet)
(O link da palestra será enviado por email aos interessados)
Titulo: Equações diferenciais parciais e as desigualdades de Harnack
Palestrante: Ruan Cardoso (aluno do curso de graduação em matemática - UFBA)
Orientador: Dirk Erhard (UFBA)

Carl Gustav Axel von Harnack (1851 – 1888) 
Exemplo da desigualdade de Harnack em que uma função harmônica (verde), sobre um disco de raio R (azul), é limitada por uma função (vermelho) que coincide com a função harmônica no centro e se aproxima do infinito próximo ao limite do disco. Fonte: Wikimedia Commons.
Resumo: Grandes descobertas como as desigualdades de Harnack, em homenagem ao matemático Carl Gustav Axel von Harnack, marcaram o desenvolvimento das Equações Diferenciais Parciais (EDPs). Originalmente formuladas para funções harmônicas no plano, mais tarde tornaram-se uma importante ferramenta na teoria da probabilidade. Nesta palestra, abordaremos exemplos de tal modelo no plano, mas não nos restringiremos à perspectiva analítica: serão apresentadas, também, aplicações no contexto probabilístico, para funções harmônicas não negativas de algumas classes de cadeias de Markov.
Moderador da palestra: Gustavo Cardoso
-
Segunda-feira 6 de junho - 17:00 horas (Sala virtual Google Meet)
(O link da palestra será enviado por email aos interessados)
Titulo: O teorema da completude da lógica proposicional clássica
Palestrante: Pedro Lucas Santos dos Reis (aluno do curso de graduação em matemática - UFBA)
Orientador: Marco Cerami (UFBA)
Resumo: Sintática ou semântica, eis a questão. Acostumamo-nos com o uso das tabelas-verdade no estudo introdutório da lógica proposicional clássica. Mas o que elas de fato significam e o que nos assegura a confiabilidade de seu uso? A resposta para essa pergunta está na compreensão da completude da lógica proposicional clássica, que estabelece a equivalência entre a dedução sintática e a consequência semântica. Nesse caso, uma vez provada a completude da lógica, podemos reduzir a análise de proposições de diversas naturezas a seus possíveis valores-verdade. Uma importante consequência disso, é que tornamos a lógica, então, computável (através das tabelas-verdade). A palestra resume-se, portanto, em demonstrar que, a partir de um conjunto de proposições, uma proposição é dedutível sse é consequência semântica.
Moderador da palestra: Ruan Cardoso
-
Segunda-feira 23 de maio - 17:00 horas (Sala virtual Google Meet)
(O link da palestra será enviado por email aos interessados)
Titulo: Transformações de Laplace
Palestrante: João Mark Souza Oliveira (aluno do curso de graduação em matemática - UFBA)
Orientador: Diego Catalano Ferraioli (UFBA)
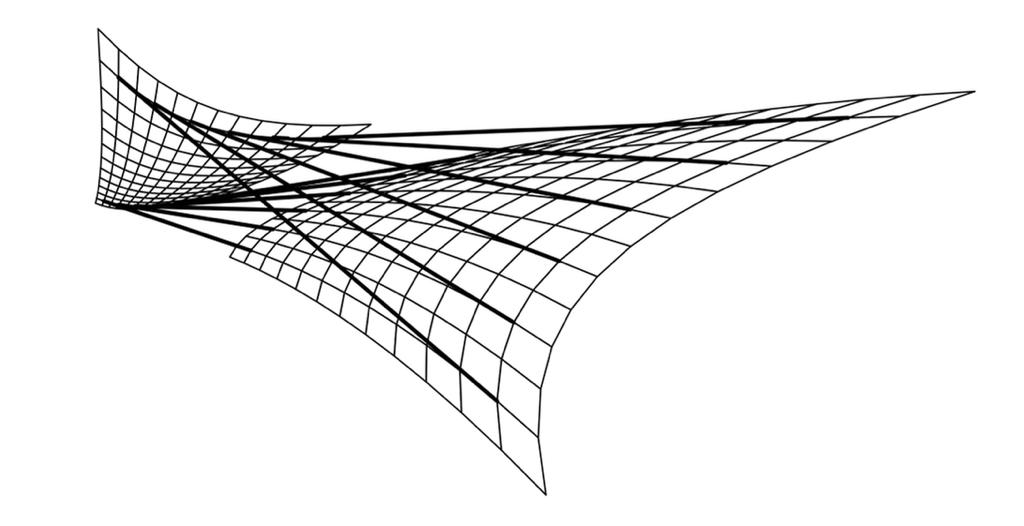
Resumo: O matemático francês G. Darboux(1842-1917), em “Leçons sur la théorie Générale des surfaces et les applications geometriques du calcul inifinitésimal” tratou pela primeira vez de um método, originalmente proposto pelo também matemático francês Laplace(1749-1827), para a integração exata de equações diferenciais lineares da forma u_xy+a(x,y)u_x+b(x,y)u_y+c(x,y)u=0, onde u=u(x,y). Essa palestra foca, precipuamente, nas equações hiperbólicas lineares. Para tal, apresentar-se-á nela as transformações de Laplace de superfícies imersas no espaço euclidiano 3-dimensional. Ulteriormente, expor-se-á aplicações das referidas transformações no estudo das equações diferenciais.
Moderador da palestra: Eldon Barros do Reis Júnior
-
Segunda-feira 9 de maio - 17:00 horas (Sala virtual Google Meet)
(O link da palestra será enviado por email aos interessados)
Titulo: O Teorema do Fluxo Tubular
Palestrante: Lucas Bandeira (aluno do curso de graduação em matemática - UFBA)
Orientador: Roberto Santanna (UFBA)
Resumo: O principal objetivo da área de Sistemas Dinâmicos é entender o comportamento assimptótico de um sistema de dados por uma transformação ou um fluxo de uma equação diferencial e as suas órbitas. O teorema do fluxo tubular nos ajuda a entender o comportamento da órbita de um ponto que não seja de equilíbrio. Para isto iremos utilizar alguns teoremas e definições importantes que nos ajudarão ao longo da apresentação.
Moderador da palestra: João Mark Souza Oliveira
-
Segunda-feira 25 de abril - 17:00 horas (Sala virtual Google Meet)
(O link da palestra será enviado por email aos interessados)
Titulo: q-Generalização da Entropia
Palestrante: Eldon Barros do Reis Júnior (aluno do curso de graduação em matemática - UFBA)
Orientador: Tertuliano Franco (UFBA)
Resumo: A entropia relativa entre medidas de probabilidade é uma ferramenta clássica em sistemas de partículas interagentes, em especial em limites de escalas de tais sistema. Neste seminário, introduziremos a entropia de Boltzmann-Gibbs, a entropia relativa entre medidas de probabilidade de Kullback-Leibler e suas principais propriedades. Além disso, mostraremos uma generalização desses funcionais no contexto da q-entropia de Tsallis referente à Mecânica Não-Extensiva, a qual contém uma noção equivalente da entropia da mecânica estatística clássica.
Moderador da palestra: Lucas Bandeira
-
Segunda-feira 11 de abril - 17:00 horas (Sala virtual Google Meet)
(O link da palestra será enviado por email aos interessados)
Titulo: Persistência de singularidades em perturbações de campos vetoriais
Palestrante: Alan Oliveira (aluno do curso de graduação em matemática - UFBA)
Orientador: Roberto Santanna (UFBA)
Resumo: Conhecer o comportamento assintótico da órbita de um ponto p, em um espaço M, sujeito a uma dinâmica f, definida em M, é um dos principais objetivos do estudo de sistemas dinâmicos. E como as singularidades são pontos de referência na descrição das órbitas de um sistema dinâmico, compreender como elas se apresentam no espaço é de grande valia. Um outro objetivo da área é verificar como uma perturbação na dinâmica f pode preservar algum comportamento da órbita de p. Nesse sentido, apresentaremos um resultado que nos garante, sob algumas condições, que a existência de uma singularidade associada a um campo vetorial é um comportamento que persiste em perturbações suaves do campo vetorial.
Moderador da palestra: Eldon Barros do Reis Júnior
-
Quarta-feira 16 de março - 17:00 horas (Sala virtual Google Meet)
(O link da palestra será enviado por email aos interessados)
Titulo: O Problema da Palavra em Grupos de Tranças
Palestrante: João Roberto Figueiredo de Almeida Mota (aluno do curso de graduação em matemática - UFBA)
Orientador: Vinicius Casteluber Laass (UFBA)
Resumo: Nesta palestra, vamos relembrar o conceito e a definição de Tranças Matemáticas e mostrar que tais objetos tem uma estrutura natural de Grupo. Vamos abordar o problema da palavra neste contexto e mostrar uma solução que envolve aspectos algébricos (apresentação de grupos) e geométricos (penteamento de tranças).
Moderador da palestra: Ugo Coutinho Monteiro de Almeida
-
Segunda-feira 28 de março - 17:00 horas (Sala virtual Google Meet)
(O link da palestra será enviado por email aos interessados)
Titulo: Lógicas Proposicionais, Semântica de Matrizes e Hierarquia de Leibniz
Palestrante: Ugo Coutinho Monteiro de Almeida (aluno do curso de graduação em matemática - UFBA)
Orientador: Darlan Pinto (UFBA)
Resumo: Abordamos o funcionamento de sistemas dedutivos (lógicas proposicionais), em diálogo com a Álgebra, estabelecendo uma interface entre esses dois campos da matemática. Primeiramente, partimos da conceituação de uma lógica abstrata como sendo um par constituído por uma álgebra de fórmulas (Fm), acrescido de uma relação de consequência invariante por substituição. Apesar de nem toda lógica poder ser representável por meios algébricos, existem diversas formas de modelá-las semanticamente através de classes de álgebras, seja equacionalmente, inequacionalmente, matricialmente etc. Este último caminho, utilizando recursos de matrizes lógicas, merece maior atenção e destaque neste trabalho, e tem como peça central o conceito do Operador de Leibniz (Ω), cujo papel se mostra extremamente significativo na classificação dos diferentes tipos de lógicas; não por acaso, o conjunto dessas classificações recebe o nome de Hierarquia de Leibniz.
Moderador da palestra: Alan Oliveira
Designed and mantained by Diego Catalano Ferraioli