Seminário ICmat 2021

Modalidade de funcionamento do seminário no semestre 2021.2

No semestre 2021.2, devido à suspensão das atividades presenciais, as palestras públicas do Seminário ICmat ocorrerão online usando o aplicativo Google Meet, preferencialmente nas segundas-feiras, das 17:00 às 18:00. Ocasionalmente, as palestras poderão ocorrer em outros dias e horários.

Para participar

Este seminário é destinado unicamente aos estudantes. Os estudantes interessados em participar do seminário deverão realizar um cadastro por meio do seguinte Formulário.

Para ministrar palestras

Os alunos interessados em apresentar uma palestra podem encaminhar uma proposta para seminarioICmat@gmail.com.

Próximas palestras

Segunda-feira 30 de agosto - 17:00 horas (Sala virtual Google Meet)
(O link da palestra será enviado por email aos interessados)

Titulo: Transição de fase no processo de contato
Palestrante: Eldon Barros (aluno do curso de graduação em matemática - UFBA)
Orientador: Tertuliano Franco (UFBA)

Resumo: O processo de contato é um modelo para propagação de uma doença sobre os vértices de um grafo. Tal modelo tem uma propriedade de dualidade que surge através da reversibilidade no tempo. Para um grafo vértice-transitivo como a rede euclidiana $d$-dimensional, há uma multiplicidade de medidas invariantes se, e somente se, houver a probabilidade estritamente positiva de existir um caminho ilimitado de infecção no espaço-tempo começando de um vértice. Essa observação permite o uso da metodologia desenvolvida para o estudo da percolação orientada. Quando o grafo subjacente é uma árvore, o modelo tem três fases distintas, extinção, sobrevivência fraca e sobrevivência forte.

Segunda-feira 6 de setembro - 17:00 horas (Sala virtual Google Meet)
(O link da palestra será enviado por email aos interessados)

Titulo: O Grupo Fundamental de um Espaço Topológico
Palestrante: Gustavo de Oliveira Cardoso dos Santos (aluno do curso de graduação em matemática - UFBA)
Orientador: Oscar Ocampo (UFBA)

Resumo: O grupo fundamental, definido pelo matemático francês Henri Poincaré em 1895, é uma ferramenta que nos possibilita, em determinadas situações, reduzir problemas topológicos à questões puramente algébricas. Neste seminário, além de definirmos o grupo fundamental de um espaço, faremos duas aplicações de tal conceito: Primeiro, o famoso Teorema do Ponto Fixo de Brouwer e por último, um resultado sobre os autovetores de matrizes com entradas reais positivas.

Moderador da palestra: Alisson Conceição

Segunda-feira 13 de setembro - 17:00 horas (Sala virtual Google Meet)
(O link da palestra será enviado por email aos interessados)

Titulo: Dinâmica: Ferraduras e Dimensão de Hausdorff
Palestrante: Alisson Conceição (aluno do curso de graduação em matemática - UFBA)
Orientador: Cristina Lizana (UFBA)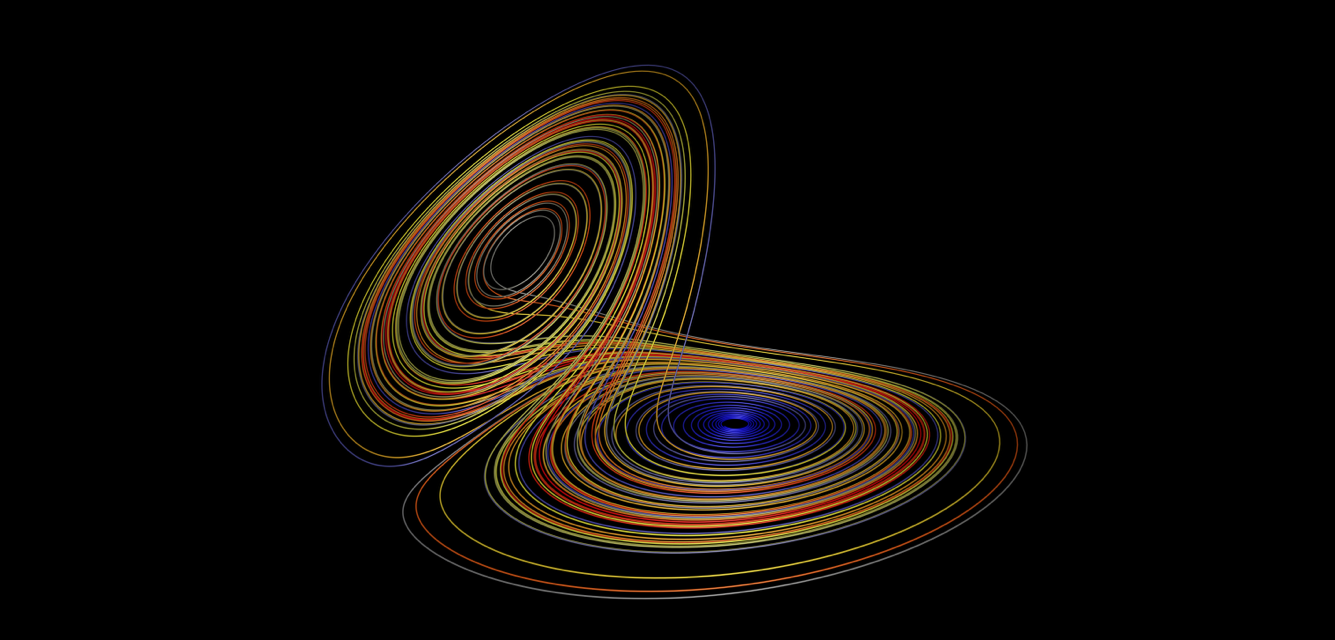

Resumo: No estudo dos Sistemas Dinâmicos podemos obter conjuntos fractais que são indistinguíveis do ponto de vista da medida. Com o intuito de diferenciar geometricamente estes conjuntos, a dimensão fractal surge como uma solução para este problema. Nesta apresentação, faremos uma introdução aos Sistemas Dinâmicos discretos, a partir de um exemplo clássico e em seguida seremos apresentados a dimensão de Hausdorff, como uma importante ferramenta para diferenciar conjuntos fractais com medida de Lebesgue nula.

Moderador da palestra: João Augusto de Moura Leite

Segunda-feira 20 de setembro - 17:00 horas (Sala virtual Google Meet)
(O link da palestra será enviado por email aos interessados)

Titulo:Simetrias de equações diferenciais e aplicações
Palestrante: João Augusto de Moura Leite (aluno do curso de graduação em matemática - UFBA)
Orientador: Diego Catalano Ferraioli (UFBA)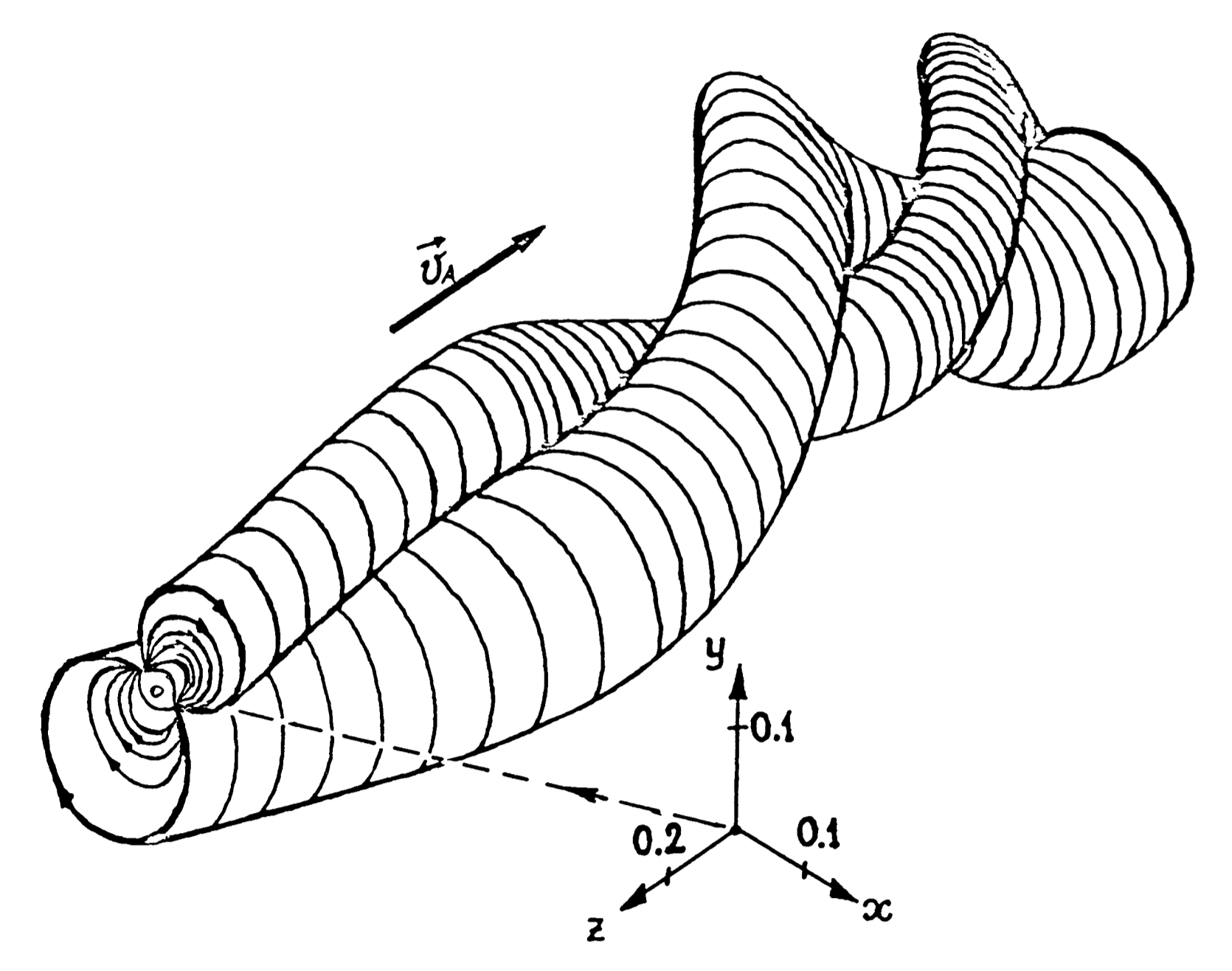

Resumo: O método das simetrias de Lie, desenvolvido por Sophus Lie no século XIX, apresenta-se como uma das mais eficientes estratégias para a integração de equações diferenciais. Nesta apresentação, iremos expor o conceito de simetria de uma equação diferencial, usando para tanto o formalismo dos espaços de jatos e as simetrias da distribuição de Cartan. Sucessivamente, iremos nos concentrar na descrição local destas simetrias e comentaremos sobre o teorema de Lie-Bäcklund, que descreve aspectos estruturais importantes das simetrias. Como mostrado pelo próprio Lie, as simetrias desempenham um papel fundamental em muitos métodos de redução e integração de equações diferenciais. Nesse sentido, no final desta apresentação, mostraremos algumas aplicações das simetrias para encontar soluções de equações diferencias.

Moderador da palestra: Michele Passos

Segunda-feira 27 de setembro - 17:00 horas (Sala virtual Google Meet)
(O link da palestra será enviado por email aos interessados)

Titulo: Mediação Causal em Análise de Sobrevivência
Palestrante: Michele Passos (aluno do curso de Estatística - UFBA)
Orientador: Leila Amorim (UFBA)

Resumo: Recentemente tem havido um aumento na aplicação da estrutura de respostas potenciais (contrafactuais) à análise de mediação. Nestas situações, existe uma variável mediadora (M) que auxilia no entendimento de como duas variáveis (X e Y) estão relacionadas de modo sequencial, tal que uma variável X (independente) afeta a variável M (mediadora) que, por sua vez, afeta a variável Y (dependente). Nas ciências sociais as abordagens à análise de mediação causal com resultado de tempo até o evento estão relacionadas a contrafactuais que utilizam modelos de sobrevivência. A análise de sobrevivência é uma área da Estatística que envolve um grande número de metodologias para descrever o comportamento de variáveis obtidas em estudos longitudinais e relacionadas ao tempo de ocorrência de eventos. Os contrafactuais podem ser estimados utilizando várias abordagens (Colosimo e Giolo, 2006; Ochoa et al., 2000; VanderWeele, 2011). Aqui, estaremos interessados na abordagem baseada em modelos de regressão. A utilização de contrafactuais na classe dos modelos de sobrevivência (sendo estes, AFT, Cox e Allen) possuem interpretação causal, desde que as suposições estejam satisfeitas. Dentro deste contexto este trabalho objetiva: Estudar e sumarizar métodos para análise de mediação causal em dados de sobrevivência, incluindo sua implementação em softwares estatísticos R; e ilustrar a aplicação e interpretação dos resultados na análise de mediação causal em sobrevivência.

Moderador da palestra: Ruan Cardoso

Segunda-feira 4 de outubro - 17:00 horas (Sala virtual Google Meet)
(O link da palestra será enviado por email aos interessados)

Titulo: Introdução à Epidemiologia: modelos matemáticos epidêmicos
Palestrante: Ruan Cardoso (aluno do curso de graduação em matemática - UFBA)
Orientador: Dirk Erhard (UFBA)

Resumo: As equações diferenciais são a principal ferramenta matemática para modelar a evolução complexa sistemas, e em muitas equações que surgem nas ciências, é necessário incluir influências, seja porque o sistema considerado é verdadeiramente aleatório, ou porque as variáveis são emuladas por termos estocásticos. Isso leva a uma equação diferencial (parcial) estocástica e, ao longo de décadas, a comunidade de análise estocástica construiu ferramentas poderosas para resolver e analisar tais equações. O objetivo do estudo foi compreender a matemática dos modelos epidêmicos e métodos para sua análise estatística. Nesta apresentação, buscamos descrever a matemática por trás dos modelos determinísticos SIS (suscetível, infectado) e SIR (suscetível, infectado e recuperado), e do modelo estocástico SIR de Reed-Frost. A metodologia foi baseada em pesquisa bibliográfica. As principais referências foram os livros Differential equation models in epidemiology (2021) escrito por Flores, Marchesin, Matos e Schecter; e o livro de Tom Britton e Håkan Andersson, Stochastic Epidemic Models and their statistical analysis (2000).

Moderador da palestra: Thales Castro Oliveira

Segunda-feira 11 de outubro - 17:00 horas (Sala virtual Google Meet)
(O link da palestra será enviado por email aos interessados)

Titulo: Sistemas de Funções Iteradas
Palestrante: Thales Castro Oliveira (aluno do curso de graduação em matemática - UFBA)
Orientador: Edgar Matias (UFBA)

Resumo: Considere uma contração definida num espaço métrico completo (M,d). O teorema do ponto fixo de Banach garante a existência de um único ponto fixo atrator global. Esse teorema, apesar de ser um teorema muito importante para a matemática, nos diz que os iterados de uma contração tem um comportamento bastante simples. No entanto, quando os iterados são gerados por uma família finita de contrações, a dinâmica resultante é extremamente rica. Ao considerar uma família finita de contrações, construiremos o operador de Barnsley-Hutchinson. Tal operador possuirá um ponto fixo atrator global, chamado de atrator de Hutchinson. Esse atrator é um conjunto compacto unicamente determinado pela coleção de contrações escolhidas e ele possui várias propriedades interessantes. Uma dessas propriedades é a existência da função codificadora, que irá dar um "endereço" ou uma "identidade" para cada ponto do atrator. Outra propriedade é conhecida como "o jogo do caos". Basicamente, ao pegarmos um ponto qualquer do espaço e iterá-lo infinitamente, escolhendo aleatoriamente a função que iremos iterar em cada passo, a órbita desse ponto, gerada pelas funções escolhidas, se acumulará em torno do atrator de Hutchinson.

Moderador da palestra: João Mark Souza Oliveira

Segunda-feira 18 de outubro - 17:00 horas (Sala virtual Google Meet)
(O link da palestra será enviado por email aos interessados)

Titulo: Transformações de Bäcklund associadas às pseudoesferas
Palestrante: João Mark Souza Oliveira (aluno do curso de graduaçã em matemática - UFBA)
Orientador: Diego Catalano Ferraioli (UFBA)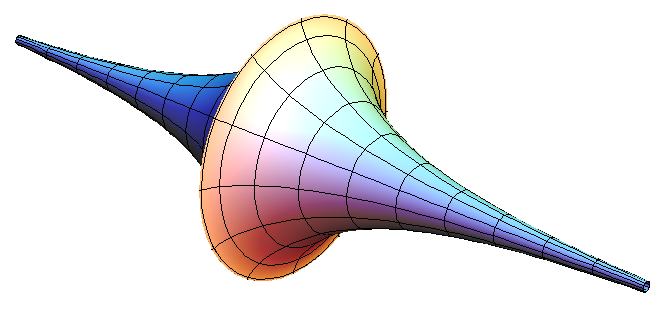

Resumo: O objetivo dessa palestra é introduzir as transformações de Bäcklund relacionadas às superfícies de curvatura gaussiana constante negativa, denominadas superfícies pseudoesféricas, no espaço euclidiano tridimensional. No final do século XIX, o matemático sueco A.V. Bäcklund (1845-1922) mostrou que era possível obter uma superfície pseudoesférica a partir de outra mediante integração de um sistema de equações diferenciais, chamado Transformação de Bäcklund. Ademais, ver-se-á que a teoria das transformações de Bäckund pode ser interpretada analiticamente através da correspondência entre superfícies pseudoesféricas e soluções da equação de Sine-Gordon. Por fim, apresentar-se-á o Teorema da Permutabilidade de L. Bianchi (1856-1928), que nos fornece uma fórmula de superposição para a construção algébrica de novas soluções desta equação.

Moderador da palestra: Henrique Costa

Segunda-feira 25 de outubro - 17:00 horas (Sala virtual Google Meet)
(O link da palestra será enviado por email aos interessados)

Titulo:Método Variacional de Problemas de Valor de Contorno
Palestrante: Carlos Rocha (aluno do curso de graduaçã em matemática - UFBA)
Orientador: Henrique Costa (UFBA)

Resumo: A matemática passou por um desenvolvimento vertiginoso entre os séculos XVII e XIX, e uma das consequências foi que passou a resolver uma variedade de problemas antes não tratados de forma satisfatõria. Muitos desses problemas têm funções e não números ou figuras geométricas como soluções. Dentre os problemas que se passaram a resolver após o advento do Cálculo, um dos mais célebres foi o da corda vibrante modelada por uma equação que envolve derivadas. De modo geral, as equações diferenciais parciais são equações que surgem naturalmente em diversos problemas de modelagem matemãtica e em diversas áreas do conhecimento, como física, biologia e também na economia. Na teoria das EDP’s estamos interessados em garantir a boa colocação, existência e regularidade das soluções. Para isso, faremos uso do Método Variacional, que de forma resumida, são extensões de métodos para encontrar valores extremantes e pontos críticos do Cálculo Diferencial. Mostraremos nesta palestra como o método dá uma base sólida para a teoria de existência e unicidade de soluções de EDP's e outros problemas aplicados utilizando o famigerado Teorema de Lax-Milgram para espaços de Hilbert.

Moderador da palestra: Igor Barbosa Arouca

Segunda-feira 1 de novembro - 17:00 horas (Sala virtual Google Meet)
(O link da palestra será enviado por email aos interessados)

Titulo: As equações pseudo-esféricas e a transformação de Bäcklund
Palestrante: Igor Barbosa Arouca (aluno do curso de graduaçã em matemática - UFBA)
Orientador: Diego Catalano Ferraioli (UFBA)

Resumo: As equações diferenciais que descrevem superfícies pseudo-esféricas são, por definição, equivalentes às equações de estrutura de uma superfície com curvatura Gaussiana K= -1, para uma tripla de 1-formas diferenciais. Exemplos bem conhecidos dessas equações são a equação sine-Gordon e a equação de Korteweg-de Vries.
Para a equação sine-Gordon, em 1883, o matemático Bäcklund mostrou ser possível construir uma sequência de soluções exatas em que cada solução pode ser obtida a partir da anterior resolvendo um sistema de equações diferenciais ordinárias. Geometricamente, sendo que toda solução da sine-Gordon corresponde a uma superfície pseudo-esférica, a transformação de Bäcklund permite de determinar também uma sequência de superfícies pseudo-esféricas. Sucessivamente, sempre para a sine-Gordon, Bianchi estabeleceu em 1892 um importante princípio de sobreposição não linear para soluções exatas obtidas por meio da transformação de Bäcklund.
Desde então, outras transformações análogas àquela de Bäcklund foram descobertas para vários tipos de equações diferenciais não lineares, dentre as quais podem ser destacadas as equações pseudo-esféricas bem como aquelas esféricas.
Nesta palestra apresentaremos principalmente uma introdução às equações pseudo-esféricas, mostrando inclusive um método intrínseco que pode ser usado para identificar transformações de tipo Bäcklund para estas equações. Além disto, trataremos também das equações esféricas e discutiremos alguns exemplos.

Moderador da palestra: Marcelo Oliveira Dias

Segunda-feira 8 de novembro - 17:00 horas (Sala virtual Google Meet)
(O link da palestra será enviado por email aos interessados)

Titulo: Ideais da reta e invariantes cardinais do contínuo
Palestrante: Marcelo Oliveira Dias (aluno do curso de - UFBA)
Orientador: Samuel Gomes (UFBA)

Resumo: O argumento diagonal de Cantor nos mostra que a reta real possui uma cardinalidade estritamente maior que a dos números naturais, o que levanta naturalmente a questão sobre a existência de cardinalidades intermediárias entre as duas; a Hipótese do Contínuo, que é um dos mais célebres resultados de independência em ZFC, e tanto influencia quanto é influenciada pela existência de determinados subconjuntos da reta real. Neste seminário, iremos introduzir os σ-ideais dos conjuntos magros e dos de medida nula e apresentar alguns resultados interessantes sobre eles, assim como falar sobre as relações entre seus invariantes cardinais.

Moderador da palestra: Lucas Oliveira Lisboa de Bilhões

Terça-feira 16 de novembro - 17:00 horas (Sala virtual Google Meet)
(O link da palestra será enviado por email aos interessados)

Titulo: Estudo Categorial de Sistemas Dedutivos
Palestrante: Lucas Oliveira Lisboa de Bilhões (aluno do curso de - UFBA)
Orientador: Darlan Pinto (UFBA)

Resumo: As lógicas algebrizáveis formam uma das linhas de pesquisa mais intensivas dentro do campo da lógica matemática atualmente. Através do método introduzido por W. J. Blok e D. Pigozzi é possível relacionar um sistema dedutivo a uma classe de estruturas algébricas e, assim, obter traduções de propriedades metalógicas e algébricas, o que torna a algebrizabilidade uma propriedade muito forte. Com o interesse em explorar e formalizar traduções e construções entre sistemas dedutivos foi introduzida a categoria das lógicas. Neste seminário, iremos introduzir alguns conceitos sobre sistemas dedutivos e falaremos sobre os sistemas dedutivos algebrizáveis, em seguida veremos alguns conceitos categoriais importantes para obter propriedades a partir da categoria de lógicas e de estruturas relacionadas.

Moderador da palestra: Allan Oliveira

Segunda-feira 22 de novembro - 17:00 horas (Sala virtual Google Meet)
(O link da palestra será enviado por email aos interessados)

Titulo: Teorema de Recorrência de Poincaré
Palestrante: Alan Oliveira (aluno do curso de - UFBA)
Orientador: Roberto Santanna (UFBA)

Resumo: A Teoria Ergódica é a disciplina matemática que estuda sistemas dinâmicos munidos de medidas invariantes. Neste seminário, esses conceitos serão apresentados a partir de suas definições, bem como de exemplos que nos permitem ilustrar o Teorema de Recorrência de Poincaré. Representativo da Teoria Ergódica, o Teorema de Poincaré, cuja demonstração será apresentada, afirma o seguinte sobre o comportamento de um sistema dinâmico: dada qualquer medida invariante finita, quase todo ponto de qualquer conjunto mensurável E regressa a E um número infinito de vezes.

Moderador da palestra: Aloisio Guimarães Ribeiro

Segunda-feira 29 de novembro - 17:00 horas (Sala virtual Google Meet)
(O link da palestra será enviado por email aos interessados)

Titulo:
Palestrante: Aloisio Guimarães Ribeiro (aluno do curso de - UFBA)
Orientador: Darlan Pinto (UFBA)

Resumo: .....

Moderador da palestra: Mauricio de Santana Brito

Segunda-feira 6 de dezembro - 17:00 horas (Sala virtual Google Meet)
(O link da palestra será enviado por email aos interessados)

Titulo:
Palestrante: Mauricio de Santana Brito (aluno do curso de graduaçã em matemática - UFBA)
Orientador: Marco Cerami (UFBA)

Resumo: .....

Moderador da palestra: Juliana Medeiros Barbosa

... - 17:00 horas (Sala virtual Google Meet)
(O link da palestra será enviado por email aos interessados)

Titulo:
Palestrante: Juliana Medeiros Barbosa (aluno do curso de graduaçã em matemática - UFBA)
Orientador: Diego Catalano Ferraioli (UFBA)

Resumo: .....

Moderador da palestra: Mateus Magno

... - 17:00 horas (Sala virtual Google Meet)
(O link da palestra será enviado por email aos interessados)

Titulo:
Palestrante: Mateus Magno (aluno do curso de - UFBA)
Orientador: Dirk Erhard (UFBA)

Resumo: .....